Bobin Nedir? Yapısı Ne İşe Yarar?

Bobin nedir: Bir iletken telin üst üste veya yan yana sarılması ile üretilen devre elemanına bobin denir. Bobin, elektrik devreleri ve denklemlerde L harfi ile gösterilir. Birimi Henry (H)‘ dir.

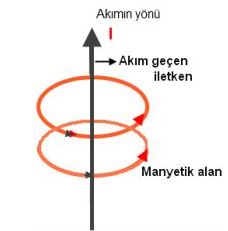
Bobine AC akım uygulandığında, akımın yönü sürekli değiştiğinden dolayı bobin etrafında bir manyetik alan oluşur. Bu manyetik alan akıma karşı ek bir direnç gösterdiğinden, AC devrelerde bobinin akıma gösterdiği direnç artar. DC devrelerde ise bobinin akıma karşı gösterdiği direnç, sadece bobinin üretildiği metalden kaynaklanan omik dirençtir.

Bobin Yapısı

Bobinin yapısında nüve (core), sipir ve mandren bulunur. Bobin endüktansını etkileyen bazı faktörler vardır. Telin sargı çapı, sargı sayısı, kalınlığı ve telin üzerine sarıldığı nüvenin fiziksel özelliği bobin endüktansını etkiler. Bobinler, çeşitli ölçü ve görünümdeki parçalar üzerine sarılır. Bobin iletkeninin üzerine sarıldığı bu parçalara karkas veya mandren denir. Bobin sarımlarında genel olarak üzeri vernikli (izoleli) bakır tel kullanılır.

Bobinlerde mandren içerisinde sabit veya hareketli bir parça daha bulunur. Bobinin mandreni içerisinde bulunan parçaya nüve denir. Mandren ve nüve kullanılmadan yapılmış bobinler de vardır. Nüve malzemesi yerine hava da olabilir. Bu çeşit bobinler hava nüveli bobinler olarak adlandırılır. Bobin telinin her bir sarımına tur, sarım veya spir denir.

Bobin; bakır, gümüş tel veya litz teli denilen ipekle yalıtılmış tel ile sarılırlar. Bir bobinin değeri tel kesitine, sarım (tur) sayısına, karkas boyuna, mandren çapına ve kullanılan nüveye (çekirdeğe) göre değişir.

Bobin DC akım altında sadece sarım telinin uzunluğundan ileri gelen omik direnç gösterir. DC gerilim ile çalışmada sargı telleri etrafında sabit manyetik alan (magnetic field) oluşur. Bu durumda bobin direnç gibi davranır. Bobinin DC’ deki direnci, sarımında kullanılan telin direnci kadardır.

AC akım altında   ise akıma karşı gösterdikleri direnç artar. Çünkü bobinde manyetik alan şiddeti değiştikçe bobinde akıma karşı koyan ek direnç etkisi meydana gelir. AC akımın salınımı (frekans) yükseldikçe akıma karşı gösterdiği direnç de yükselir.  Bobinlerin elektriksel değerine indüktans denir.

İndüktans, bobinin kendi kendini etkileme derecesidir. İndüktans birimi henry ‘dir. Bir henry, bobin üzerinden geçen 1 A değerindeki AC akımın 1 saniyedeki değişimidir. 1 voltluk zıt elektromotor kuvveti (EMK) oluşturuyorsa bu bobinin indüktansına karşılık gelen miktardır. Henry, indüktans değeri bakımında çok yüksek bir değere karşılık geldiği için uygulamalarda çoğunlukla henry ‘nin ast katları kullanılır.

1 H = 1000 milihenry = 1000000 mikrohenry

Bobin Ne İşe Yarar?

İndüktör (ınductor) üzerinden akan elektrik akımının değişimi yavaş olduğu için, güç kaynaklarında ve sinyal (signal) işleme devrelerinde filtre görevinde kullanılır. Farklı sarım sayılarına sahip iki adet bobinden meydana gelen trafolar ise, AC gerilimin yükseltilmesinde veya alçaltılmasında kullanılırlar. Ayrıca manyetik alan depolama özellikleri sayesinde indüktörler, anahtarlamalı güç kaynaklarında da kullanılır.

Bobin İle Kondansatör Arasındaki Benzerlik

Bobin ile kondansatör arasındaki benzerlik;

her iki devre elemanı  da elektrik enerjisini harcamayan reaktif devre elemanlarıdır.  Kondansatörler elektrik yüklerini depolayabilir.  Bobinler de elektrik enerjisini kısa süreliğine manyetik alan olarak depo ederler. Bobinlerin kondansatörlerde olduğu gibi AC akım ve DC akım altındaki çalışma davranışları çok farklıdır. Bu iki devre elemanı arasındaki fark ise;

kondansatör devreye bağlı iken gerilimi faz farkı (geri bırakırken), bobin ise gerilimi ileri kaydırır. Bobin ve kondansatör gerilim ve akım arasında yarattığı faz farkı uygulamada fayda ve zararlara sebep olur.

• Bobinlerde Zıt Elektromotor Kuvveti (EMK)

Bobine AC akım uygulayalım. Bobin çevresinde oluşan farklı yönlerdeki manyetik alanların bobin üzerinde iki etkisi olur.

1. Uygulanan AC akımın değerinin sıfırdan maksimum değere doğru artar. Bu artışı sırasında bobinin manyetik alanının kendisini oluşturan kuvvete karşı koyarak bu akımı azaltmaya çalışmasıdır.
2. AC akım değeri maksimum değerden sıfıra doğru azalır. Bu defa bobinin manyetik alanının kendisi üzerinde voltaj oluşturarak (indükleyerek) akımın azalışını yavaşlatmaya çalışmasıdır.

İkinci etki sırasında bobinin manyetik alanının kendisi üzerinde oluşturduğu gerilime zıt EMK denir. Bobinler zıt EMK ile akımın geçişini geciktirir ve AC özellikli akımların 90º geri kalmasına sebep olurlar.

• Bobin Endüktansını Etkileyen Faktörler

Endüktans ölçümü ile ilgili detaylı bilgi için sayfamızı ziyaret edebilirsiniz.

• Sarım sayısı,
• Nüvenin cinsi,
• Tel kesiti,
• Bobinin biçimi,
• Bobin çapı,
• Sargı katı sayısı,
• Sarımlar arası aralık,
• Sargı tipi,
• Uygulanan AC akımın frekansı.

gibi etkenler endüktans (inductance) değerini değiştiren faktörlerdir.

• Bobinlerin AC ve DC Akım Karşısında Davranışları

Bir bobine DC akım uygulandığı zaman indüktif bir akım oluşmaz. Sadece sabit bir manyetik alan oluşur. Bu manyetik alana yaklaştırılan nikel, demir, kobalt gibi maddeler bobin tarafından çekilir. İçinde nüve olmayan bobinlerin çekim gücü az olur.

Bir bobine AC akım uygulandığında, sarım çevresinde farklı manyetik alan oluşur. Bu alanlardan dolayı akım dolanımına engel olan bir etki ortaya çıkar. Bobinin indüktansına bağlı olarak değişen karşı koyma şiddetine indüktif reaktans denir.

Bobin Çeşitleri

Sabit ve ayarlı olmak üzere iki tip bobin çeşidi vardır. Bobin çeşitleri detaylı bilgi için sayfamızı ziyaret edebilirsiniz.

Bobinin Kullanım Alanları

Bobinin elektrik ve elektronikte yaygın bir kullanım alanı vardır.

• Isıtıcı vb
• Hoparlörler
• Motorlar
• Röleler (relay)
• Solenoidler
• Trafolar
• Doğrultucular da şok bobini
• Elektromıknatıslar
• Zil, elektromagnetik vinç
• Numaratör
• Kontaktör
• Analog ölçü aleti
• Osilatör
• Balast
• İndüktif metal sensörleri
• Yüksek frekans devrelerinde  (havalı bobin)
• Radyolarda ferrit anten elemanı (Uzun, orta, kısa dalga bobini)
• Telekomünikasyonda frekans ayarı (ayarlı göbekli bobin)